Honestly I have trouble dealing with the fact that others (like you) are very eloquent, while I am just a babbling buffoon. It is difficult
someacnt_
True nathematician would never make a mistake distinguishing finite and infinite cardinality. Countability, on the other hand.. (but that's a separate issue)
Easy, view it on a curved display. Now every line is curved
If only haskell devs were writing documentations, instead of going "type sigs is all the documentation you need!"
I see. Maybe learning mathematics have screwed my writing since so much of mathematical literature is simply equations, definitions and propositions. Lots of papers, and even books, are just bad at expositions, in my experience.
It takes hours to write essays for me..
There is no good programming language, even including the ones people do not use.
I wish I were you, I struggle so much with reading books and papers
They do have antiderivatives, you just cannot elementarily compute them. Non-exact differential forms, however..
Seems like one can maybe work with complex metric. Interesting idea
I am sorry, but.. to be pedantic, pythagorean theorem works on real-valued length. Complex numbers can be scalars, but one does not use it for length for some reason I forgor.
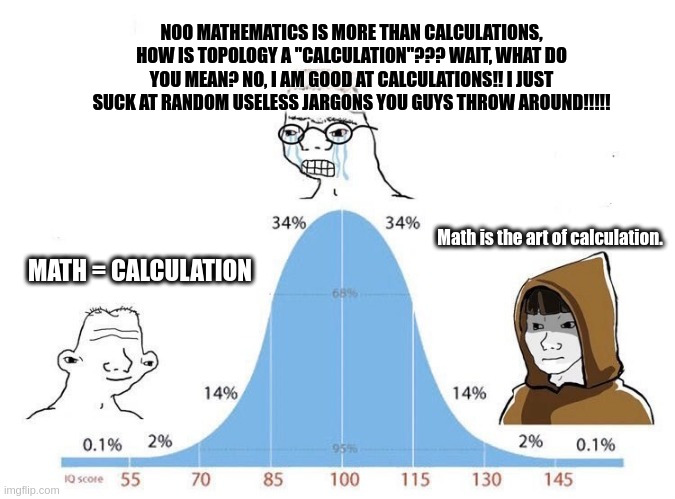






Counting cohomology has done to me a numbers x_x