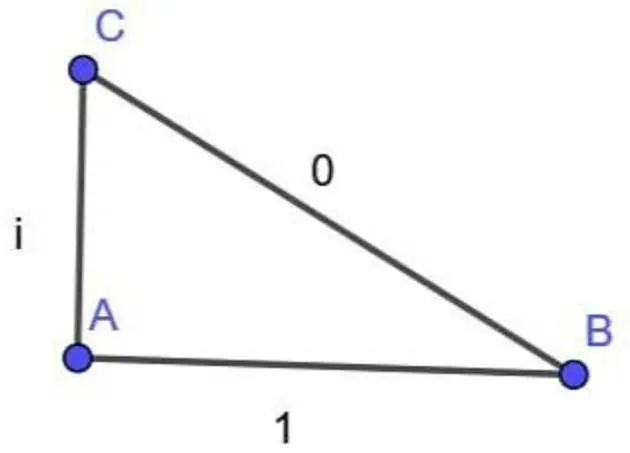
Imaginary numbers always feel wrong
Science Memes
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- !reptiles and [email protected]
Physical Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and [email protected]
- [email protected]
- !self [email protected]
- [email protected]
- [email protected]
- [email protected]
Memes
Miscellaneous
I never really appreciated them until watching a bunch of 3blue1brown videos. I really wish those had been available when I was still in HS.
After watching a lot of Numberphile and 3B1B videos I said to myself, you know what, I'm going back to college to get a maths degree. I switched at last moment to actuarial sciences when applying, because it's looked like a good professional move and was the best decision on my life.
After delving into quaternions, complex numbers feel simple and intuitive.
after you spend enough time with complex numbers, the real numbers start to feel wrong
Can we all at least agree that counting numbers are a joke? Sometimes they start at zero … sometimes they start at one …
ISO 80000-2 defines 0 as a natural number. qed.
If you are comfortable with negative numbers, then you are already comfortable with the idea that a number can be tagged with an extra bit of information that represents a rotation. Complex numbers just generalize the choices available to you from 0 degrees and 180 degrees to arbitrary angles.
You need to add some disclaimer to this diagram like "not to scale"...
It's to scale.
Which scale is left as an exercise to the reader.
I really don't think it is.
Yeah, 1 and i should be the same size. It’s 1 in the real dimension and 1 in the imaginary dimension creating a 0 but anywhere you see this outside pure math it’s probably a sinusoid
I may not have been entirely serious
This is why a length of a vector on a complex plane is |z|=√(z×z). z is a complex conjugate of z.
I've noticed that, if an equation calls for a number squared, they usually really mean a number multiplied by its complex conjugate.
[ you may want to escape the characters in your comment... ]
Isn't the squaring actually multiplication by the complex conjugate when working in the complex plane? i.e., √((1 - 0 i) (1 + 0 i) + (0 - i) (0 + i)) = √(1 + - i^2^) = √(1 + 1) = √2. I could be totally off base here and could be confusing with something else...
Almost:
Lengths are usually reals, and in this case the diagram suggests we can assume that A is the origin wlog (and the sides are badly drawn vectors without a direction)
Next we convert the vectors into lengths using the abs function (root of conjugate multiplication). This gives us lengths of 1 for both.
Finally, we can just use a Euclidean metric to get our other length √2.
Squaring isn't multiplication by complex conjugate, that's just mapping a vector to a scalar (the complex | x | function).
I think you're thinking of taking the absolute value squared, |z|^2 = z z*
Considering we're trying to find lengths, shouldn't we be doing absolute value squared?
It’s just dimensionally shifted. This is not only true, its truth is practical for electrical engineering purposes. Real and imaginary cartesians yay!
This is pretty much the basis behind all math around electromagnetics (and probably other areas).
Would you explain how, for a simpleton?
The short version is: we use some weird abstractions (i.e., ways of representing complex things) to do math and make sense of things.
The longer version:
Electromagnetic signals are how we transmit data wirelessly. Everything from radio, to wifi, to xrays, to visible light are all made up of electromagnetic signals.
Electromagnetic waves are made up of two components: the electrical part, and the magnetic part. We model them mathematically by multiplying one part (the magnetic part, I think) by the constant i, which is defined as sqrt(-1). These are called "complex numbers", which means there is a "real" part and a "complex" (or "imaginary") part. They are often modeled as the diagram OP posted, in that they operate at "right angles" to each other, and this makes a lot of the math make sense. In reality, the way the waves propegate through the air doesn't look like that exactly, but it's how we do the math.
It's a bit like reading a description of a place, rather than seeing a photograph. Both can give you a mental image that approximates the real thing, but the description is more "abstract" in that the words themselves (i.e., squiggles on a page) don't resemble the real thing.
Makes sense, thanks. More of a data transmission than an electrical power thing.
Circles are good at math, but what to do if you not have circle shape? Easy, redefine problem until you have numbers that look like the numbers the circle shape uses. Now we can use circle math on and solve problems about non-circles!
Now calculate the angles
That's actually pretty easy. With CB being 0, C and B are the same point. Angle A, then, is 0, and the other two angles are undefined.
No thank you

Doesn't this also imply that i == 1 because CB has zero length, forcing AC and AB to be coincident? That sounds like a disproving contradiction to me.
I think BAC is supposed to be defined as a right-angle, so that AB²+AC²=CB²
=> AB+1²=0²
=> AB = √-1
=> AB = i
Too complexe for me ;)
you are imagining things
The length would be equal to the absolute value
What if not a Hilbert space?