this post was submitted on 08 Oct 2024
1120 points (98.2% liked)
People Twitter
5226 readers
2344 users here now
People tweeting stuff. We allow tweets from anyone.
RULES:
- Mark NSFW content.
- No doxxing people.
- Must be a tweet or similar
- No bullying or international politcs
- Be excellent to each other.
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
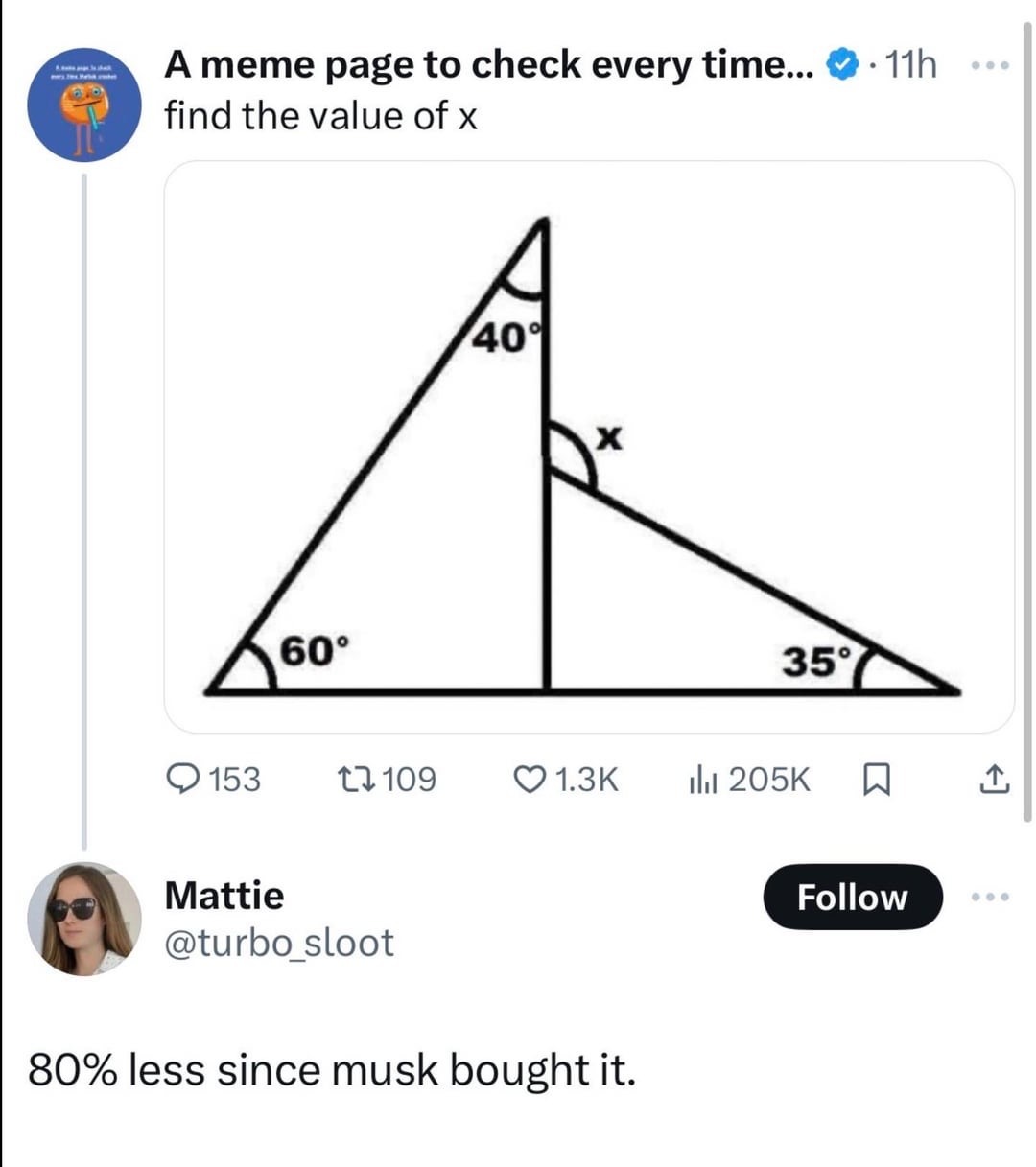
135
It pisses me off to no end that what is CLEARLY shown as a 90degree angle is not in fact 90deg, I hate it when they do that.
Also I will sadly admit this can teach people lessons about verifying the information themselves.
^GrumbleGrumbleGrumble....^
I get you, but it doesn't clearly indicate the angle in the middle at the base as much as it suggestively waggles its eyebrows towards 90⁰, it could just as easily be 89.9999999999999⁰, although upon zooming in, you can see the line does shift one pixel over on its way up. You simply can't trust any of the angles as 90⁰ unless it's got the ∟ symbol (that's the official unicode) or you've measured them yourself, and with that one pixel off-set, it's decidedly not 90⁰. That's why you have to do the math.
The internal angles of a triangle always add up to 180⁰, therefore the one pixel offset is irrelevant because the unlabelled angle is, despite what the image suggests, ~~60~~ 80⁰.
Assuming you're talking about the triangle on the left, it's 80⁰:
180 - 60 - 40 = 80. The other two unlabeled angles are 100⁰ and 45⁰ respectively. None of the unlabelled angles are 60⁰.The shape on the left might be a quadrilateral instead of a triangle, with a vertex at the same place as the top vertex of the shape on the right.
Yes I meant 80 lol, thanks
It's enough to say it's "CLEARLY" not 90⁰.
That's just what I said but more into the weeds on the detail.
👍
Geometry diagrams in math problems should never be assumed to be to scale
Yes obviously. But it still irritates me as someone who does geometry for a living.
Another way to look at it is that it is simply a representation of an object. We don't need to visualize the angles, as the values to the other asks are given. We just need the geometry of the object represented so we can calculate the value of the unlabeled angle. Given that the geometry of the objects is represented as triangles, we can infer that all sides are straight lines, regardless of the type of space the object occupies.
Actually, it might be a 90 degree angle, but the shape on the left might be a quadrilateral instead of a triangle.
Assuming these are straight lines.
Even if they are straight lines, if that's a 2d projection of something on a non-flat 3d surface, it can also change the way the angles fit together.
If these aren't straight lines, drag has no idea what the answer is and thinks it might be impossible to tell.